这个问题其实已经老生常谈了,它也是面试里面的高频问题,要理解它的原理其实并不复杂,下面请跟着我一起来探寻产生这个问题的根源吧

javascript里是如何存储数字的
我们知道,对于计算机来说,它并不认识类似0.1和0.2这样的数字的,它只认识0、1 二进制串,因此要想对数字进行运算,首先得将数字转化为2进制串并保存在计算机里才行
不同的语言采取了不同的存储方式来存储数字,在js里整数和小数都是 Number 类型,并且都是采用 IEEE 754 标准下的 双精度浮点数格式 进行存储,也就是用 64位 来存储数字,这个64位里分为三部分,列举如下:
- sign bit(S,符号):用来表示正负号,0 为 正 1 为 负(1 bit)
- exponent(E,指数):用来表示次方数(11 bits)
- mantissa(M,尾数):用来表示精确度 (52 bits)
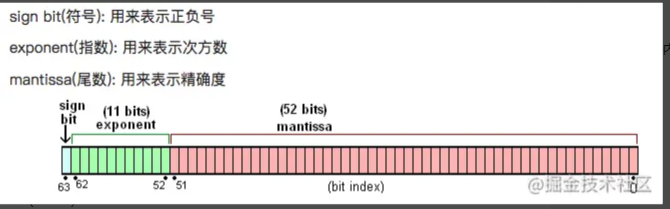
需要注意的是,对于尾数来说,默认第一位为1,可以省略,因此实际可表示的尾数为 53 bits
精度的第一次丢失
有了上面的知识,我们先将0.1和0.2转为2进制
- 0.1: 00011001100110011001(1001)…
- 0.2: 00110011001100110011(0011)…
可以看到,0.1和0.2转换为2进制时,是一个 无限循环的 数字
计算机肯定不能存一个无限循环的数字,此时就会进行 精度截取,从上文我们知道,js里的尾数位最多52位,因此会根据进1舍0的原则进行截取,只保留 52位 的有效位数,注意,此时是 第一次 精度丢失
下面以0.1为例,说明下具体的转换过程,首先贴一个公式
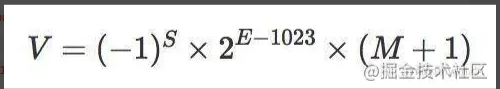
精度位总共是 53 bit,因为用科学计数法表示,所以首位固定的 1 就没有占用空间。即公式中 (M + 1) 里的 1。另外公式里的 1023 是 2^11 的一半,e小于 1023 的用来表示小数,大于 1023 的用来表示整数
首先0.1转为二进制 00011001100110011001(1001)…,用科学技术法表示为 1.100110011… x 2^(-4),通过公式可知S 为 0(1 bit),E为 1023 - 4 = 1019,对应二进制位 01111111011(11 bits),M为 1001100110011001100110011001100110011001100110011010(52 bits)
精度的第二次丢失
在0.1和0.2各自得到它们的近似值之后,由于指数位数不同,运算时需要进行对阶运算。具体的计算过程我也没有细究,但需要知道的一点是在这个过程中有 舍入 的操作,因此这也会 再一次 造成精度的丢失,最终呈现的结果就是我们所看到的 0.1 + 0.2 = 0.30000000000000004了

杂谈
通过上文,我们知道了在js里进行四则运算时,其结果不一定是可靠的。这一节将列出js里提供的特殊number,它们可以在一定程度上辅助我们在日常开发中避免数值计算不可靠的问题
- Number.EPSILON: 两个可表示(representable)数之间的最小间隔,对于0.1+0.2是否等于0.3的问题,我们可以通过
0.1+0.2-0.3 < Number.EPSILON来解决 - Number.MAX_SAFE_INTEGER: JavaScript 中最大的安全整数 2^53 - 1
- Number.MIN_SAFE_INTEGER: JavaScript 中最小的安全整数 -(2^53 - 1)
- Number.MAX_VALUE: 能表示的最大正数。最小的负数是 -MAX_VALUE
- Number.MIN_VALUE: 能表示的最小正数即最接近 0 的正数 (实际上不会变成 0)。最大的负数是 -MIN_VALUE
结语
其实0.1+0.2 !== 0.3的问题不只是js里有,只要任何使用了IEEE 754的规范的语言都会存在这个问题,因此不能让js来背锅,而我们要做的是透过现象看本质,这样才能不被表象所迷惑,从而成为一个优秀的工程师~
